
Isi kandungan:
- Pengarang Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:39.
- Diubah suai terakhir 2025-01-22 17:06.
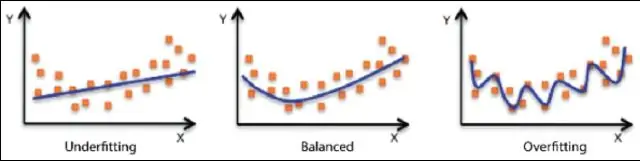
Regresi tak linear boleh sesuai dengan lebih banyak jenis lengkung, tetapi ia boleh memerlukan lebih banyak usaha untuk mencari yang terbaik dan untuk mentafsir peranan pembolehubah bebas. Selain itu, R-squared tidak sah untuk regresi tak linear , dan adalah mustahil untuk mengira nilai-p untuk anggaran parameter.
Dengan cara ini, bolehkah regresi menjadi tak linear?
Dalam statistik, regresi tak linear adalah satu bentuk regresi analisis di mana data pemerhatian dimodelkan oleh fungsi iaitu a tak linear gabungan parameter model dan bergantung pada satu atau lebih pembolehubah bebas. Data dipasang dengan kaedah anggaran berturut-turut.
Seseorang juga mungkin bertanya, adakah r kuasa dua hanya untuk regresi linear? Rangka kerja matematik am untuk R - kuasa dua tidak berfungsi dengan betul jika model regresi tidak linear . Walaupun isu ini, kebanyakan perisian statistik masih mengira R - kuasa dua untuk model tak linear. Jika anda menggunakan R - kuasa dua untuk memilih yang terbaik model , ia membawa kepada yang sepatutnya model sahaja 28-43% masa.
Mengenai ini, bagaimana anda mengira regresi bukan linear?
Jika model anda menggunakan persamaan dalam bentuk Y = a0 + b1X1, ianya adalah regresi linear model. Jika tidak, ia adalah tak linear.
Y = f(X, β) + ε
- X = vektor p peramal,
- β = vektor bagi parameter k,
- f(-) = fungsi regresi yang diketahui,
- ε = istilah ralat.
Apakah jenis regresi?
Jenis Regresi
- Regresi Linear. Ia adalah bentuk regresi yang paling mudah.
- Regresi Polinomial. Ia adalah teknik untuk menyesuaikan persamaan tak linear dengan mengambil fungsi polinomial pembolehubah bebas.
- Regresi Logistik.
- Regresi Kuantil.
- Regresi Permatang.
- Regresi Lasso.
- Regresi Bersih Elastik.
- Regresi Komponen Utama (PCR)
Disyorkan:
Adakah fungsi linear atau bukan linear?

Fungsi linear ialah fungsi dengan bentuk piawai y = mx + b, dengan m ialah cerun dan b ialah pintasan-y, dan grafnya kelihatan seperti garis lurus. Terdapat fungsi lain yang grafnya bukan garis lurus. Fungsi ini dikenali sebagai fungsi tak linear dan ia datang dalam pelbagai bentuk
Bolehkah anda menggunakan sin dan cos pada segi tiga bukan tegak?

Pertimbangkan satu lagi segitiga bukan tegak, dilabelkan seperti yang ditunjukkan dengan panjang sisi x dan y. Kita boleh memperoleh undang-undang berguna yang mengandungi hanya fungsi kosinus. Hukum kosinus boleh digunakan untuk mencari ukuran sudut atau sisi segitiga bukan tegak jika kita tahu: tiga sisi dan tiada sudut
Bagaimanakah anda melakukan regresi sinusoidal pada kalkulator?
VIDEO Di sini, bagaimana anda mengira regresi sinusoidal? Regresi Sinusoid . Laraskan nilai A, B, C dan D dalam persamaan y = A*sin(B(x-C))+D untuk membuat a sinusoidal lengkung sesuai dengan set data yang dijana secara rawak. Sebaik sahaja anda mempunyai fungsi yang baik, klik pada "
Bolehkah kita menggunakan hukum ketiga Newton pada daya graviti?
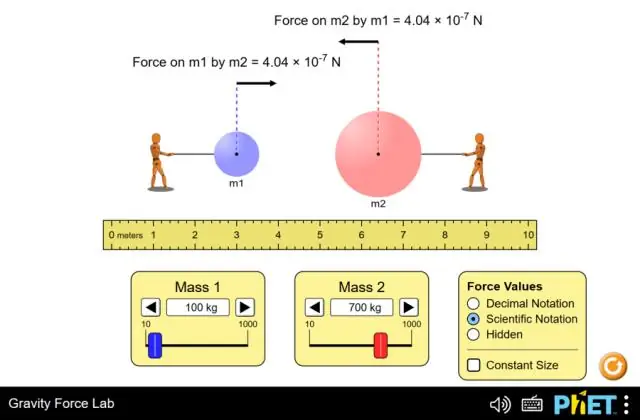
Ya, undang-undang ketiga Newton boleh digunakan untuk daya graviti. Oleh itu, Ini bermakna apabila bumi kita mengenakan daya tarikan pada objek, maka objek itu juga mengenakan daya yang sama di bumi, dalam arah yang bertentangan. Oleh itu kita boleh mengatakan bahawa anda boleh menggunakan hukum ketiga Newton kepada daya graviti
Bagaimanakah anda mengetahui sama ada persamaan adalah linear atau bukan linear?

Menggunakan Persamaan Permudahkan persamaan sedekat mungkin kepada bentuk y = mx + b. Semak untuk melihat sama ada persamaan anda mempunyai eksponen. Jika ia mempunyai eksponen, ia adalah tak linear. Jika persamaan anda tidak mempunyai eksponen, ia adalah linear
