Video: Adakah garis selari bersilang dalam geometri hiperbolik?
2024 Pengarang: Miles Stephen | [email protected]. Diubah suai terakhir: 2023-12-15 23:39
Dalam geometri hiperbolik , terdapat dua jenis garis selari . Jika dua baris lakukan bukan bersilang dalam model geometri hiperbolik tetapi mereka saling bersilang pada sempadannya, kemudian garisan dipanggil asimptotik selari atau hiperparallel.
Begitu juga, orang bertanya, adakah garis selari bersilang pada sfera?
Garis selari boleh tidak wujud dalam berbentuk sfera geometri. Mana-mana lurus barisan melalui titik P pada a sfera adalah mengikut definisi bulatan yang hebat. Dua bulatan hebat akan bersilang pada dua titik pada segmen Euclidean, iaitu diameter bagi sfera . Tidak ada selari dalam berbentuk sfera geometri.
Juga, bolehkah garis selari bersilang? Dalam geometri projektif, mana-mana pasangan garisan sentiasa bersilang pada satu ketika, tetapi garis selari jangan bersilang dalam pesawat sebenar. The barisan pada infiniti isadded kepada pesawat sebenar. Ini melengkapkan pesawat, kerana sekarang garis selari bersilang pada satu titik yang terletak pada barisan pada infiniti.
Tambahan pula, berapa banyak garis selari dalam geometri hiperbolik?
Matematik di Sebalik Fakta: Dua garisan dikatakan selari jika mereka tidak bersilang. Dalam bahasa Euclidean geometri , diberi a barisan L ada betul-betul satu barisan melalui mana-mana diberi titik Piaitu selari kepada L (yang selari postulat). Walau bagaimanapun dalam geometri hiperbolik , ada tak terhingga manylines selari ke L melalui P.
Mengapakah garis selari tidak wujud dalam geometri elips?
Dalam bentuk sfera geometri Garis selari JANGAN WUJUD . Dalam bahasa Euclidean geometri suatu postulat wujud menyatakan bahawa melalui satu titik, di sana wujud hanya 1 selari kepada yang diberikan barisan . Oleh itu, Garis selari jangan wujud kerana mana-mana kalangan besar ( barisan ) melalui satu titik mesti bersilang dengan bulatan besar asal kita.
Disyorkan:
Apabila rentas bersilang dua garis selari yang manakah pasangan sudut adalah kongruen?
Jika rentas bersilang dua garis selari, maka sudut pedalaman silih ganti adalah kongruen. Jika rentas bersilang dua garis selari, maka sudut pedalaman sisi yang sama adalah tambahan
Adakah sepasang garis bersilang menentukan satah?
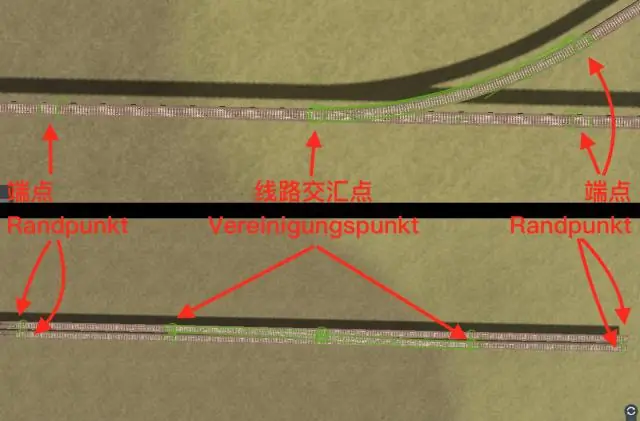
'Jika dua garis bersilang, maka tepat satu satah mengandungi garisan itu.' 'Jika dua garis bersilang, maka ia bersilang tepat pada satu titik.' dan tiga titik tak kolinear mentakrifkan satah
Apakah garis bersilang selari dan garis serenjang?
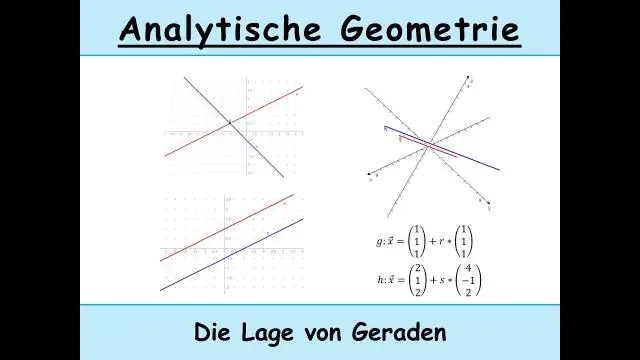
Apakah garis bersilang selari dan garis serenjang? A. Garis selari ialah garisan dalam satah yang jaraknya sentiasa sama. Garis serenjang ialah garis yang bersilang pada sudut tepat (90 darjah)
Adakah masuk akal untuk mencari persamaan garis selari dengan garis tertentu dan melalui titik pada garis yang diberikan?
Persamaan garis yang selari atau berserenjang dengan garis tertentu? Jawapan yang mungkin: Kecerunan garis selari adalah sama. Gantikan cerun yang diketahui dan koordinat titik pada garis lain ke dalam bentuk cerun titik untuk mencari persamaan garis selari
Adakah garis selari bertemu dalam infiniti?
Dalam geometri unjuran, mana-mana pasangan garis sentiasa bersilang pada satu titik, tetapi garis selari tidak bersilang dalam satah sebenar. Garis atinfinity ditambah pada satah sebenar. Ini melengkapkan satah, kerana kini garis selari bersilang pada satu titik yang terletak pada garisan pada infiniti