
- Pengarang Miles Stephen [email protected].
- Public 2023-12-15 23:39.
- Diubah suai terakhir 2025-01-22 17:06.
A bulatan adalah 360° sepanjang jalan; oleh itu, jika anda membahagikan an arka ukuran darjah sebanyak 360°, anda dapati pecahan bagi bulatan lilitan yang arka make up. Kemudian, jika anda mendarab panjang sepanjang jalan di sekeliling bulatan (yang bulatan lilitan) dengan pecahan itu, anda mendapat panjang sepanjang arka.
Dengan cara ini, apakah formula untuk panjang lengkok bulatan?
Untuk mencari panjang lengkok , mulakan dengan membahagikan arka sudut pusat dalam darjah dengan 360. Kemudian, darabkan nombor itu dengan jejari bagi bulatan . Akhir sekali, darab nombor itu dengan 2 × pi untuk mencari panjang lengkok . Jika anda ingin belajar cara mengira panjang lengkok dalam radian, teruskan membaca artikel itu!
Begitu juga, bagaimana anda mencari arka? Jika sudut lengkok anda diukur dalam darjah maka gunakan formula ini untuk mengira panjang lengkok:
- Panjang arka (A) = (Θ ÷ 360) x (2 x π x r)
- A = (Θ ÷ 360) x (D x π)
- A = Panjang arka.
- Θ = Sudut lengkok (dalam darjah)
- r = jejari bulatan.
- A = r x Θ
- A = panjang lengkok.
- r = jejari bulatan.
Begitu juga, anda mungkin bertanya, apakah lengkok bulatan?
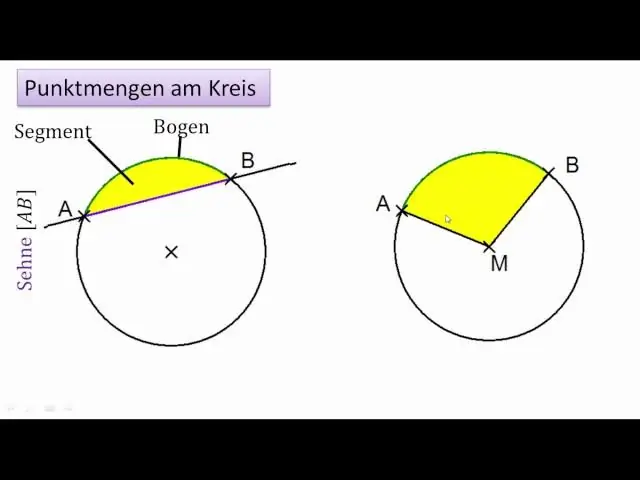
An arka ialah sebahagian daripada lilitan a bulatan . Dalam rajah di atas, arka ialah bahagian biru bulatan . Tegasnya, an arka boleh menjadi sebahagian daripada beberapa bentuk melengkung lain, seperti elips, tetapi ia hampir selalu merujuk kepada a bulatan . Untuk mengelakkan semua kemungkinan kesilapan, ia kadang-kadang dipanggil pekeliling arka.
Lengkok manakah ialah separuh bulatan?
Dalam matematik (dan lebih khusus geometri), a separuh bulatan ialah lokus titik satu dimensi yang membentuk separuh bulatan. yang penuh arka daripada a separuh bulatan sentiasa mengukur 180° (setara, π radian, atau separuh pusingan). Ia hanya mempunyai satu garis simetri (simetri pantulan).
Disyorkan:
Bagaimanakah anda mencari panjang lengkok dan luas sektor?

Sudut pusat yang dicangkum oleh lengkok utama mempunyai ukuran lebih besar daripada 180°. Formula panjang lengkok digunakan untuk mencari panjang lengkok bulatan; l=rθ l = r θ, di mana θ berada dalam radian. Kawasan sektor didapati A=12θr2 A = 1 2 θ r 2, di mana θ berada dalam radian
Berapakah bilangan lengkok yang boleh dilukis dalam bulatan?
Diameter bulatan membahagikannya kepada dua lengkok yang sama. Setiap lengkok dikenali sebagai separuh bulatan. Jadi, terdapat dua separuh bulatan dalam bulatan penuh. Ukuran darjah bagi setiap separuh bulatan ialah 180 darjah
Apakah lengkok utama bulatan?

Lengkok utama (angka kanan) ialah lengkok bulatan yang mempunyai ukuran lebih besar daripada atau sama dengan (radian). LIHAT JUGA: Lengkok, Lengkok Kecil, Separuh Bulatan
Berapakah panjang lengkok bulatan?

Lengkok bulatan ialah 'bahagian' lilitan bulatan. Panjang lengkok hanyalah panjang 'bahagian' lilitannya. Sebagai contoh, ukuran lengkok 60º ialah satu perenam daripada bulatan (360º), jadi panjang lengkok itu ialah satu perenam daripada lilitan bulatan
Berapakah bilangan darjah lengkok dalam lengkok kecil?

Lengkok minor ialah lengkok yang lebih kecil daripada separuh bulatan. Sudut pusat yang dicangkum oleh lengkok kecil mempunyai ukuran kurang daripada 180°. Kord, sudut pusat atau sudut tersurat boleh membahagikan bulatan kepada dua lengkok. Yang lebih besar daripada dua lengkok dipanggil lengkok utama
