Video: Apakah contoh nombor rasional yang bukan nombor bulat?
2024 Pengarang: Miles Stephen | [email protected]. Diubah suai terakhir: 2023-12-15 23:39
A rasional ” nombor ialah nisbah antara dua integer. Untuk contoh , berikut adalah nombor rasional , dan tiada satu pun daripada mereka adalah integer: 1/2. 2/3.
Soalan juga ialah, apakah nombor rasional yang bukan nombor bulat?
Semua integer negatif ialah nombor rasional tetapi mereka adalah bukan nombor bulat . Contohnya -3 ialah a nombor rasional (boleh dinyatakan sebagai -3/1), tetapi ia adalah bukan nombor bulat . Pecahan seperti 1/2, -3/4, 22/7 dll.
Kedua, adakah negatif 3 nombor rasional? − 3 adalah negatif jadi ia bukan semula jadi atau keseluruhan nombor . Nombor rasional adalah nombor yang boleh dinyatakan sebagai pecahan atau nisbah dua integer. Nombor rasional ditandakan Q. Sejak − 3 boleh ditulis sebagai − 3 1, boleh dikatakan bahawa − 3 adalah juga nyata nombor.
Kedua, apakah nombor rasional yang merupakan nombor bulat?
Setiap nombor bulat ialah nombor rasional : contohnya, 3=31. Jadi ia adalah rasional . Setiap nombor bulat n boleh ditulis sebagai pecahan integer: n=n1. Kami tidak perlu menulisnya seperti itu; kita hanya perlu tahu bahawa ia adalah mungkin untuk menyatakan setiap nombor bulat sebagai pecahan integer, dan oleh itu ia adalah rasional.
Bolehkah nombor rasional menjadi nombor bulat tetapi bukan integer?
Set nombor bulat = {0, 1, 2, 3, 4, …} Nombor bulat adalah adil integer yang bukan negatif. Menggunakan tatatanda set, kita boleh mengatakan bahawa set daripada integer ialah manakala set daripada nombor bulat pada dasarnya adalah. Jadi kembali kepada soalan; Tidak , terdapat tiada nombor rasional yang bukan integer tetapi ialah nombor bulat.
Disyorkan:
Apakah nombor asli dan nombor bulat dengan contoh?
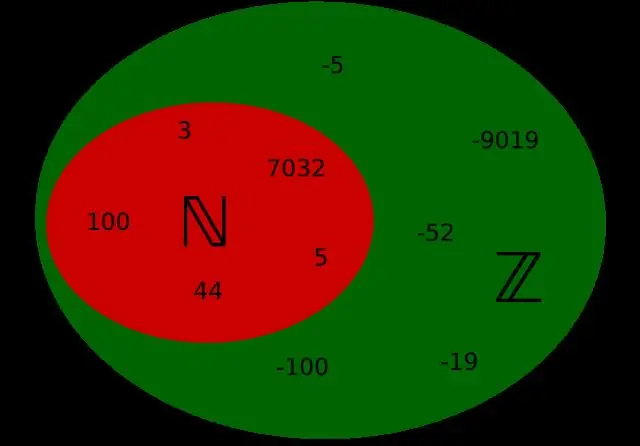
Nombor asli ialah semua nombor 1, 2, 3, 4… Ia adalah nombor yang biasanya anda kira dan ia akan berterusan sehingga ke infiniti. Nombor bulat adalah semua nombor asli termasuk 0 cth. 0, 1, 2, 3, 4… Nombor bulat termasuk semua nombor bulat dan rakan sejawatan negatifnya cth.
Apakah jenis nombor yang membentuk set nombor yang dipanggil nombor nyata?
Set Nombor Nyata (integer positif) atau nombor bulat {0, 1, 2, 3,} (integer bukan negatif). Ahli matematik menggunakan istilah 'semula jadi' dalam kedua-dua kes
Apakah nombor asli nombor bulat integer dan nombor rasional?
Nombor nyata terutamanya dikelaskan kepada nombor rasional dan tidak rasional. Nombor rasional termasuk semua integer dan pecahan. Semua integer negatif dan nombor bulat membentuk set integer. Nombor bulat terdiri daripada semua nombor asli dan sifar
Nombor yang manakah bukan sepunya antara nombor asli dan nombor bulat?
Sifar tidak mempunyai nilai positif atau negatif. Walau bagaimanapun, sifar dianggap sebagai nombor bulat, yang seterusnya menjadikannya integer, tetapi tidak semestinya nombor asli
Apakah jenis perpuluhan nombor tak rasional berikan contoh?
Nombor ini termasuk perpuluhan yang tidak ditamatkan, tidak berulang (pi, 0.45445544455544445555, 2, dsb.). Mana-mana punca kuasa dua yang bukan punca sempurna ialah nombor tidak rasional. Sebagai contoh, 1 dan 4 adalah rasional kerana 1 = 1 dan 4 = 2, tetapi 2 dan 3 adalah tidak rasional-tiada kuasa dua sempurna antara 1 dan 4