Video: Bagaimanakah anda melakukan eksponen dengan nombor negatif?
2024 Pengarang: Miles Stephen | [email protected]. Diubah suai terakhir: 2023-12-15 23:39
Sekiranya nombor negatif dinaikkan kepada kuasa ganjil, hasilnya akan menjadi negatif . The nombor negatif mesti disertakan dengan kurungan untuk mempunyai eksponen memohon kepada negatif istilah. Eksponen ditulis sebagai superskrip nombor (cth. 34) atau didahului oleh tanda karet (^)simbol (cth. 3^4).
Selain itu, bagaimanakah anda memudahkan pecahan dengan eksponen negatif?
The pecahan dengan eksponen negatif dalam penyebut boleh dipermudahkan dengan mengalihkan sebutan bagi eksponen negatif dalam sebarang susunan daripada penyebut kepada pembilang dan menjadi positif eksponen . Iaitu, dan, yang bermaksud bahawa a eksponen negatif adalah sama dengan timbal balik positif berlawanan eksponen.
Tambahan pula, apa yang berlaku apabila eksponen adalah negatif? A eksponen negatif hanya bermakna bahawa asas mengisarkan bahagian yang salah pada garis pecahan, jadi anda perlu menterbalikkan pangkalan ke bahagian lain. Sebagai contoh, "x–2" (disebut sebagai "ecks to the minustwo") hanya bermaksud "x2, tetapi di bawah, seperti dalam 1 x 2frac{1}{x^2} x21 ".
Juga perlu diketahui, apakah peraturan untuk menduakan nombor negatif?
Malah, apa-apa nombor sama sekali boleh kuasa dua , malah nombor seperti pi dan 0. Ini kerana untuk segi empat sama anumber hanya bermaksud untuk mendarabkannya dengan sendirinya. Contohnya, (-2) kuasa dua ialah (-2)(-2) = 4. Perhatikan bahawa ini adalah positif kerana apabila anda mendarab dua nombor negatif anda mendapat keputusan yang positif.
Apakah peraturan eksponen sifar?
Apabila anda mempunyai nombor atau pembolehubah dinaikkan kepada kuasa, nombor (atau pembolehubah) dipanggil asas, manakala nombor superskrip dipanggil eksponen , atau kuasa. The peraturan sifar eksponen pada asasnya mengatakan bahawa mana-mana asas dengan eksponen daripada sifar adalah sama dengan satu. Contohnya: x^0 =1.
Disyorkan:
Bagaimanakah anda menulis semula eksponen negatif?
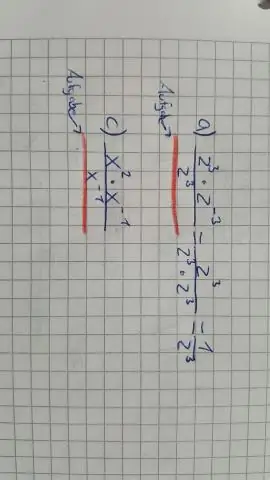
Untuk menulis semula eksponen negatif sebagai eksponen positif, ambil salingan asas a. Tekan di sini. Lihat ungkapan dan cari eksponen negatif. Untuk menulis semula eksponen negatif sebagai eksponen positif, ambil salingan asas
Apakah jenis nombor yang membentuk set nombor yang dipanggil nombor nyata?
Set Nombor Nyata (integer positif) atau nombor bulat {0, 1, 2, 3,} (integer bukan negatif). Ahli matematik menggunakan istilah 'semula jadi' dalam kedua-dua kes
Apakah nombor asli nombor bulat integer dan nombor rasional?
Nombor nyata terutamanya dikelaskan kepada nombor rasional dan tidak rasional. Nombor rasional termasuk semua integer dan pecahan. Semua integer negatif dan nombor bulat membentuk set integer. Nombor bulat terdiri daripada semua nombor asli dan sifar
Mengapakah punca kubus bagi nombor negatif ialah nombor negatif?
Punca kubus nombor negatif akan sentiasa negatif Memandangkan kubus nombor bermakna menaikkannya kepada kuasa ke-3-yang ganjil- punca kubus nombor negatif juga mestilah negatif. Apabila suis dimatikan (biru), hasilnya negatif. Apabila suis dihidupkan (kuning), hasilnya adalah positif
Bagaimanakah anda melakukan integer negatif?
Untuk bekerja dengan integer negatif, kita mesti mengikut satu set peraturan: Peraturan #1: Apabila menambah positif dan negatif, tidak seperti tanda, tolak nombor dan berikan jawapan tanda nilai mutlak yang lebih besar (berapa jauh dari sifar a nombor ialah)