Isi kandungan:
Video: Bagaimanakah anda menilai fungsi komposit?
2024 Pengarang: Miles Stephen | [email protected]. Diubah suai terakhir: 2023-12-15 23:39
Menilai Fungsi Komposit Menggunakan Graf
- Cari input yang diberikan ke dalam fungsi pada paksi-x grafnya.
- Baca keluaran dalaman fungsi daripada paksi-y grafnya.
- Cari bahagian dalam fungsi keluaran pada paksi-x graf bahagian luar fungsi .
Di sini, bagaimana anda menulis dan menilai fungsi komposit?
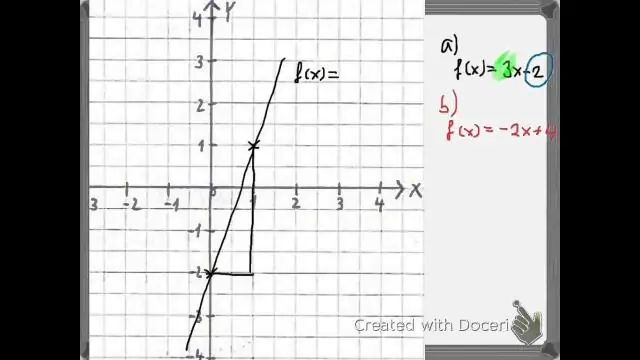
Untuk membuat a fungsi komposit di mana kita meletakkan g(x) di dalam fungsi f(x), kita boleh menulis ia f(g(x)). Perhatikan bahawa bukannya hanya meletakkan x dalam fungsi , kita gantikan keseluruhan g(x) fungsi . Apabila kita berbuat demikian, kita mempunyai f(g(x)) = (3x) + 2. Di sebelah kiri, anda akan melihat bahawa g fungsi berada di dalam f fungsi.
Begitu juga, apakah contoh fungsi komposit? A fungsi komposit ialah fungsi itu bergantung kepada yang lain fungsi . A fungsi komposit dicipta apabila satu fungsi digantikan dengan yang lain fungsi . Untuk contoh , f(g(x)) ialah fungsi komposit yang terbentuk apabila g(x) digantikan dengan x dalam f(x). Di dalam gubahan (f ο g)(x), domain bagi f menjadi g(x).
Orang ramai juga bertanya, apakah langkah-langkah untuk menyelesaikan fungsi komposit?
Berikut adalah langkah-langkah kita boleh gunakan untuk mencari gubahan daripada dua fungsi : Langkah 1: Tulis semula gubahan dalam bentuk yang berbeza. Sebagai contoh, yang gubahan (f g)(x) perlu ditulis semula sebagai f(g(x)). Langkah 2: Gantikan setiap kejadian x yang terdapat di luar fungsi dengan bahagian dalam fungsi.
Apakah yang dimaksudkan dengan fungsi komposit?
: a fungsi yang nilainya didapati daripada dua yang diberikan fungsi dengan mengaplikasikan satu fungsi kepada pembolehubah bebas dan kemudian menggunakan yang kedua fungsi kepada hasil dan domainnya terdiri daripada nilai-nilai pembolehubah bebas yang hasilnya dihasilkan oleh yang pertama fungsi terletak dalam domain kedua.
Disyorkan:
Bagaimanakah anda mendarabkan fungsi komposit?
Pendaraban dan Komposisi Fungsi Untuk mendarab fungsi dengan skalar, darab setiap keluaran dengan skalar itu. Apabila kita mengambil f (g(x)), kita mengambil g(x) sebagai input bagi fungsi f. Sebagai contoh, jika f (x) = 10x dan g(x) = x + 1, maka untuk mencari f (g(4)), kita dapati g(4) = 4 + 1 + 5, dan kemudian menilai f (5 ) = 10(5) = 50. Contoh: f (x) = 2x - 2, g(x) = x2 - 8
Bagaimanakah anda mencari isipadu prisma komposit?
Bentuk komposit pertama ialah gabungan prisma segi empat tepat dan piramid. Untuk mencari isipadu keseluruhan bentuk anda mencari isipadu setiap bentuk individu dan menambahnya bersama-sama. Rajah kedua terdiri daripada silinder dan hemisfera
Apakah fungsi komposit dalam kalkulus?
Menggabungkan dua (atau lebih) fungsi seperti ini dipanggil mengarang fungsi, dan fungsi yang terhasil dipanggil fungsi komposit. Peraturan fungsi komposit menunjukkan kepada kita cara yang lebih cepat. Peraturan 7 (Peraturan fungsi komposit (juga dikenali sebagai peraturan rantai)) Jika f(x) = h(g(x)) maka f (x) = h (g(x)) × g (x)
Apakah susunan yang betul untuk menilai ungkapan algebra?
Agar matematik berfungsi, hanya ada satu perintah operasi untuk menilai ungkapan matematik. Susunan operasi ialah Kurungan, Eksponen, Pendaraban dan Pembahagian (dari kiri ke kanan), Penambahan dan Penolakan (dari kiri ke kanan)
Bagaimanakah anda tahu jika fungsi adalah fungsi kuasa?
VIDEO Begitu juga, orang bertanya, apakah yang menjadikan fungsi sebagai fungsi kuasa? A fungsi kuasa ialah fungsi dengan y = x ^n dengan n ialah sebarang nombor pemalar nyata. Ramai ibu bapa kita fungsi seperti linear fungsi dan kuadratik fungsi sebenarnya fungsi kuasa .