Isi kandungan:
Video: Bagaimanakah anda membuktikan wau dalam geometri koordinat?
2024 Pengarang: Miles Stephen | [email protected]. Diubah suai terakhir: 2023-12-15 23:39
Berikut ialah dua kaedah:
- Jika dua pasang belah sisi yang berturutan bagi sebuah segiempat adalah kongruen, maka ia adalah layang-layang (sebaliknya layang-layang definisi).
- Jika salah satu pepenjuru segiempat ialah pembahagi dua serenjang bagi yang lain, maka ia adalah layang-layang (sebalik harta).
Seterusnya, mungkin ada yang bertanya, apakah ciri-ciri wau?
layang-layang sifat termasuk (1) dua pasang sisi kongruen berturut-turut, (2) sudut bukan bucu kongruen dan (3) pepenjuru serenjang. Sifat poligon penting lain yang perlu diketahui termasuk sifat trapezoid, sifat selari, sifat rombus, dan sifat segi empat tepat dan segi empat sama.
Juga Ketahui, adakah segi empat tepat berserenjang? Seperti yang anda boleh lihat dari gambar di sebelah kiri, pepenjuru a segi empat tepat jangan bersilang dalam sudut yang betul (mereka tidak berserenjang ). (Melainkan jika segi empat tepat ialah segi empat sama.) Dan sudut-sudut yang dibentuk oleh persilangan tidak selalunya sama ukuran (saiz). Sudut pusat bertentangan adalah saiz yang sama (ia adalah kongruen.)
Seterusnya, persoalannya ialah, adakah wau serenjang?
DEFINISI: A layang-layang ialah segiempat yang empat sisinya dilukis sedemikian rupa sehingga terdapat dua set yang berbeza bersebelahan, kongruen sisi. TEOREM: Jika segi empat ialah layang-layang , pepenjuru ialah berserenjang . TEOREM: Jika segi empat ialah layang-layang , ia mempunyai sepasang sudut bertentangan kongruen.
Adakah segi empat tepat ialah segi empat selari?
A segi empat tepat mempunyai dua pasang sisi bertentangan selari, dan empat sudut tegak. Ia juga merupakan a segi empat selari , kerana ia mempunyai dua pasang sisi selari.
Disyorkan:
Bagaimanakah anda mencari Preimage dalam geometri?
Imej T(V) ditakrifkan sebagai set {k | k=T(v) untuk beberapa v dalam V}. Jadi x=T(y) dengan y ialah unsur T^-1(S). Praimej S ialah set {m | T(m) berada dalam S}. Oleh itu T(y) berada dalam S, jadi oleh kerana x=T(y), kita mempunyai bahawa x berada dalam S
Bagaimanakah anda membuktikan garis selari dalam pembuktian?
Yang pertama ialah jika sudut yang sepadan, sudut yang berada pada sudut yang sama pada setiap persimpangan, adalah sama, maka garisan adalah selari. Yang kedua ialah jika sudut pedalaman berselang-seli, sudut-sudut yang berada di sisi bertentangan rentas rentas dan di dalam garis selari, adalah sama, maka garisan itu selari
Apakah bukti yang menggunakan rajah pada satah koordinat untuk membuktikan sifat geometri?
Bukti yang menggunakan rajah pada satah koordinat untuk membuktikan sifat geometri dirujuk sebagai trigonometri
Bagaimanakah anda mendapatkan kunci oren dalam sengkang geometri?
Dengan memasukkan frasa tertentu, ganjaran Kit Ikon dan pencapaian yang berkaitan boleh dibuka kuncinya. Pada mulanya, terdapat dada di sudut kanan bawah yang mengandungi kunci oren untuk kunci oren di Basement
Bagaimanakah anda membina satah koordinat dalam geometri?
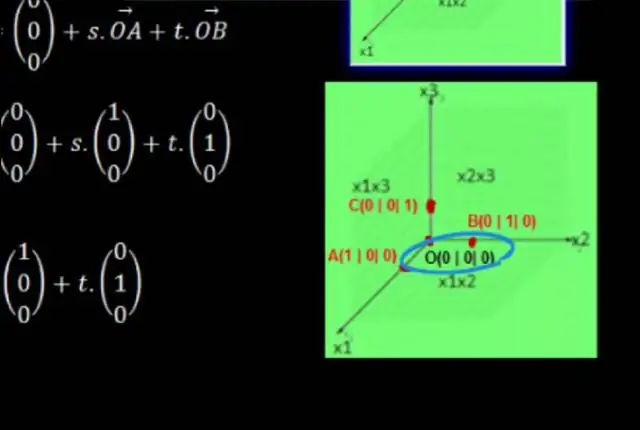
Untuk mencipta satah koordinat, kita ikuti langkah berikut: Lukis dua garis nombor berserenjang antara satu sama lain, bersilang pada titik 0 pada kedua-dua garis. Labelkan garis nombor mendatar sebagai paksi-x dan labelkan garis nombor menegak sebagai paksi-y