Isi kandungan:
Video: Bagaimanakah anda mencari pintasan ketaksamaan?
2024 Pengarang: Miles Stephen | [email protected]. Diubah suai terakhir: 2023-12-15 23:39
Sebagai alternatif, kita boleh menentukan x- memintas dan mereka- memintas daripada bentuk standard linear ketidaksamaan dengan menggantikan y = 0, kemudian selesaikan x dan gantikan x = 0, kemudian selesaikan masing-masing untuk y. Ingat bahawa thex- memintas ialah nilai x apabila y = 0 dan mereka- memintas ialah nilai y apabila x = 0.
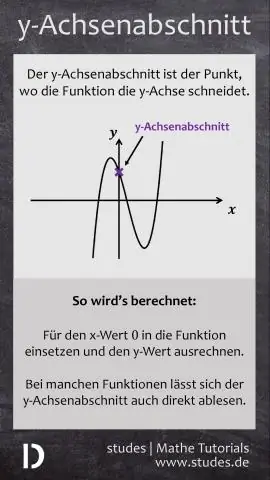
Di sini, bagaimana anda mencari pintasan Y bagi ketaksamaan?
Awak boleh cari yang y - memintas dengan melihat graf dan melihat titik yang melintasi y paksi. Titik ini akan sentiasa mempunyai x koordinat sifar. Ini satu lagi cara untuk mencari yang y - memintas , jika awak mengetahui persamaan, yang y - memintas ialah penyelesaian kepada persamaan apabila x = 0. Mari cari persamaan untuk baris ini.
Juga, bagaimana anda menyusun semula ketaksamaan linear? Cara Graf Ketaksamaan Linear
- Susun semula persamaan supaya "y" berada di sebelah kiri dan segala-galanya di sebelah kanan.
- Plot garisan "y=" (jadikan garis padat untuk y≤ ory≥ dan garis putus-putus untuk y)
- Lorekkan di atas garisan untuk "lebih besar daripada" (y> atau y≥)atau di bawah garisan untuk "kurang daripada" (y< atau y≤).
Dengan cara ini, apakah penyelesaian kepada ketidaksamaan?
"Menyelesaikan'' an ketidaksamaan bermakna mencari segala-galanya penyelesaian . A" penyelesaian '' daripada sebuah ketidaksamaan ialah bilangan yang apabila digantikan dengan pembolehubah menjadikan ketidaksamaan kenyataan yang benar. Apabila kita menggantikan 8 dengan x, maka ketidaksamaan menjadi 8-2 > 5. Oleh itu, x=8 ialah a penyelesaian daripada yang ketidaksamaan.
Bagaimanakah anda menyelesaikan ketaksamaan kuadratik?
Untuk menyelesaikan ketaksamaan kuadratik, ikuti langkah berikut:
- Selesaikan ketaksamaan seolah-olah ia adalah persamaan.
- Jadikan titik sempadan bulatan pepejal jika ketaksamaan asal termasuk kesamaan; jika tidak, buat bulatan mata sempadan terbuka.
- Pilih titik daripada setiap kawasan yang dibuat oleh titik sempadan.
Disyorkan:
Bagaimanakah anda mencari cerun dengan pintasan?
Bentuk pintasan cerun ialah bentuk y = mx + b, dengan m mewakili cerun, dan b mewakili pintasan mereka. Jadi jika persamaan garis ialah y = 3/4 x - 2, maka garis itu ditulis dalam bentuk pintasan cerun, atau y = bentuk mx+ b, dengan m = 3/4 dan b = -2
Bagaimanakah anda membuat graf ketaksamaan pada satah koordinat?
Terdapat tiga langkah: Susun semula persamaan supaya 'y' berada di sebelah kiri dan semua yang lain di sebelah kanan. Plot garis 'y=' (jadikan garis pepejal untuk y≤ atau y≥, dan garis putus-putus untuk y) Lorekkan di atas garisan untuk 'lebih besar daripada' (y> atau y≥) atau di bawah garisan untuk 'kurang daripada' (y< atau y≤)
Bagaimanakah anda menulis bentuk pintasan cerun dalam bentuk standard?
Bentuk piawai ialah cara lain untuk menulis bentuk pintasan cerun (berbanding dengan y=mx+b). Ia ditulis sebagai Ax+By=C. Anda juga boleh menukar bentuk pintasan cerun kepada bentuk standard seperti ini: Y=-3/2x+3. Seterusnya, anda mengasingkan pintasan-y (dalam kes ini ialah 2) seperti ini: Tambahkan 3/2x pada setiap sisi persamaan untuk mendapatkan ini: 3/2x+y=3
Bagaimanakah anda mencari pintasan cerun daripada jadual?
Untuk mencari pintasan-y, gantikan cerun dalam untuk m dalam formula y = mx + b, dan gantikan pasangan tertib yang diberi dalam jadual untuk x dan y dalam formula, kemudian selesaikan untuk b. Akhir sekali, gantikan nilai bagi m dan b ke dalam formula y = mx + b untuk menulis persamaan garis
Bagaimanakah anda menulis persamaan dalam bentuk pintasan cerun untuk jadual?
Ambil persamaan y = mx + b dan palamkan nilai m (m = 1) dan sepasang koordinat (x, y) daripada jadual, seperti (5, 3). Kemudian selesaikan b. Akhir sekali, gunakan nilai m dan b yang anda temui (m = 1 dan b = -2) untuk menulis persamaan