Isi kandungan:
Video: Bagaimanakah anda menggunakan pembahagian sintetik untuk mencari hasil bahagi?
2024 Pengarang: Miles Stephen | [email protected]. Diubah suai terakhir: 2023-12-15 23:39
VIDEO
Dengan mengambil kira perkara ini, bagaimanakah anda mencari dividen pembahagi dan hasil bahagi menggunakan pembahagian sintetik?
Pembahagian Sintetik oleh x − a
- 47 = 9· 5 + 2.
- Dividen = Sebutharga· Pembahagi + Baki.
- P(x) = Q(x)· D(x) + R(x).
- Turunkan pekali pendahulu (1), darab dengan (2), dan. tulis produk itu (1· 2) dalam lajur kedua:
- Ulangi proses tersebut. −3· 2 = −6.
- Penyelesaian.
- P(x) = Q(x)· D(x) + R.
Begitu juga, bagaimana anda menyelesaikan masalah pembahagian sintetik? Pembahagian sintetik ialah cara lain untuk membahagi polinomial dengan binomial x - c, dengan c ialah pemalar.
- Langkah 1: Sediakan bahagian sintetik.
- Langkah 2: Turunkan pekali pendahulu ke baris bawah.
- Langkah 3: Darab c dengan nilai yang baru ditulis pada baris bawah.
- Langkah 4: Tambahkan lajur yang dibuat dalam langkah 3.
Juga untuk mengetahui, apakah kaedah pembahagian sintetik?
Pembahagian sintetik ialah pintasan, atau pintasan, kaedah daripada pembahagian polinomial dalam kes khas pembahagian dengan faktor linear -- dan ia hanya berfungsi dalam kes ini. Pembahagian sintetik biasanya digunakan, walau bagaimanapun, bukan untuk membahagikan faktor tetapi untuk mencari sifar (atau punca) polinomial. Lebih lanjut mengenai perkara ini kemudian.
Apakah pembahagian sintetik dan contohnya?
Pembahagian sintetik ialah kaedah trengkas membahagi polinomial untuk kes khas membahagi dengan faktor linear yang pekali pendahulunya ialah 1. Untuk menggambarkan proses, ingat semula contoh pada permulaan bahagian. Bahagikan 2x3−3x2+4x+5 2 x 3 − 3 x 2 + 4 x + 5 dengan x+2 menggunakan panjang pembahagian algoritma.
Disyorkan:
Apakah proses pembahagian sel dalam eukariota yang paling serupa dengan pembahagian sel dalam prokariot?
Tidak seperti eukariota, prokariot (yang termasuk bakteria) menjalani sejenis pembahagian sel yang dikenali sebagai pembelahan binari. Dalam beberapa aspek, proses ini serupa dengan mitosis; ia memerlukan replikasi kromosom sel, pengasingan DNA yang disalin, dan pembelahan sitoplasma sel induk
Bagaimanakah anda menggunakan nombor yang serasi untuk menganggarkan pembahagian?
Ringkasan Nombor yang serasi ialah nombor yang hampir dengan nombor yang mereka gantikan yang membahagi sama rata antara satu sama lain. Hasil bagi ialah hasil yang anda dapat apabila anda membahagi. 56,000 hampir kepada 55,304. 800 hampir dengan 875, DAN ia membahagi sama rata kepada 56,000
Bagaimanakah anda menggunakan peraturan tangan kanan untuk hasil silang?
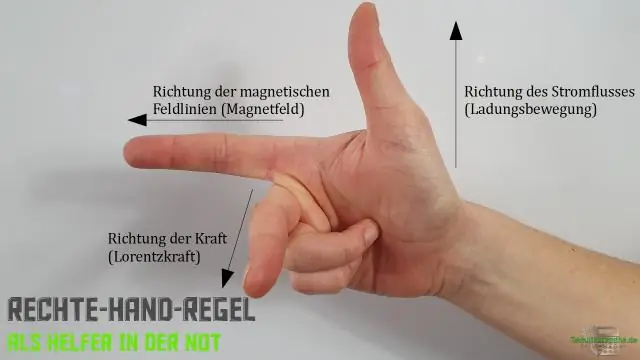
Peraturan tangan kanan menyatakan bahawa orientasi hasil silang vektor ditentukan dengan meletakkan dan ekor-ke-ekor, meratakan tangan kanan, memanjangkannya ke arah, dan kemudian melencongkan jari ke arah yang dibuat sudut. Ibu jari kemudian menunjuk ke arah
Bagaimanakah anda membahagi dengan hasil bahagi separa?
Langkah 1: Tulis senarai fakta mudah untuk pembahagi. Langkah 2: Tolak daripada dividen gandaan mudah pembahagi (cth. 100x, 10x, 5x, 2x). Catatkan hasil bahagi separa dalam lajur di sebelah kanan masalah. Langkah 3: Ulang sehingga dividen telah dikurangkan kepada sifar atau bakinya kurang daripada pembahagi
Bagaimanakah anda menggunakan pendaraban untuk mencari hasil bahagi?
Dalam pendaraban nombor yang anda darab dipanggil faktor; jawapannya dipanggil produk. Dalam pembahagian nombor yang dibahagikan ialah dividen, nombor yang membahagikannya ialah pembahagi, dan jawapannya ialah hasil bagi